Supporting classes and routines for FourthOrderMappedFineInterp. More...

#include <cstring>
#include "NamespaceHeader.H"
#include "NamespaceFooter.H"

Include dependency graph for FourthOrderMappedFineInterpSup.H:

Classes
class	CoordTransform
	Coordinate transformations. More...

Macros
#define	_FOURTHORDERMAPPEDFINEINTERPSUP_H_

Functions
int	binomial (const int n, int k)
	Calculate a binomial coefficient. More...

int	powerIndex (int a_m, IntVect a_p)
	Find the sequential index of a power. More...

Detailed Description

Supporting classes and routines for FourthOrderMappedFineInterp.

Macro Definition Documentation

◆ _FOURTHORDERMAPPEDFINEINTERPSUP_H_

#define _FOURTHORDERMAPPEDFINEINTERPSUP_H_

Function Documentation

◆ binomial()

int binomial	(	const int	n,
		int	k
	)

inline

Calculate a binomial coefficient.

Parameters

[in]	n
[in]	k

Returns: Binomial coefficient

References CH_assert.

Referenced by powerIndex().

◆ powerIndex()

int powerIndex	(	int	a_m,
		IntVect	a_p
	)

inline

Find the sequential index of a power.

The powers are indexed as follows (i.e for 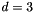$d=3$ dimensions)

*     int idx = 0
*     for (px = 0; px <= m; ++px)
*       for (py = 0; px+py <= m; ++py)
*         for (pz = 0; px+py+pz <= m; ++py)
*           ++idx

where 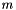$m$ is the degree of the polynomial and we wish to find idx. To compute the sequential index of any given power, we can use the relations

$\mbox{number of powers} = {m + d \choose d}$

and

$\sum_{j=k}^n {j\choose k} = { n+1 \choose k+1 }$

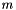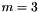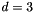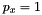With these, the amount to add to the sequential index for a power at a spatial index is total number of powers remaining at this spatial index (remainder of $m$ ) minus the number of powers not used at this spatial index. E.g, if $m=3$ , $d=3$ , and $p_x=1$ , there are 2 powers left for the remaining 2 dimensions,

${2+2 \choose 2}\,.$

The increment to the sequential index is then

${2+3+1 \choose 2+1} - {2+2+1 \choose 2+1}$

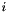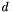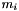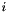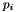In general, this can be written for direction index $i$ , in $d$ space dimensions, with $m_i$ giving the remaining available powers at $i$ , and $p_i$ giving the power used at index 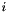$i$ as