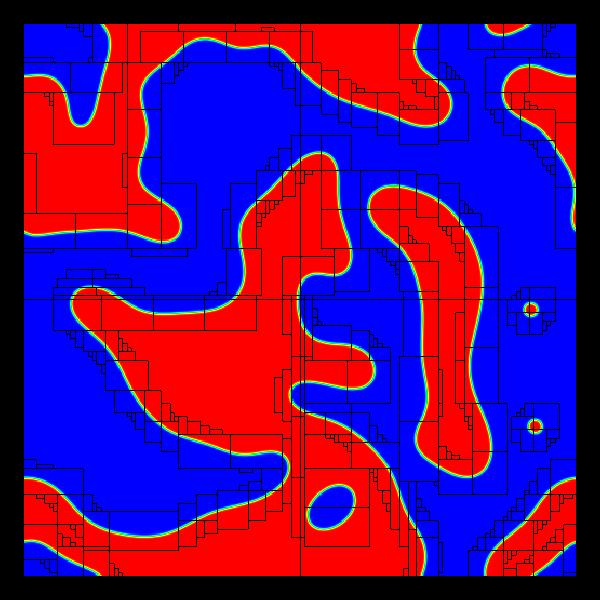
The time-dependent Ginszberg-Landau equation is a diffusion equation with a nonlinear source term. It is a model for phase-field dynamics (for example, crystal growth in metals).

Here we show the evolution of a phase field with random initial conditions (which could represent a heated metal, for example). The solution evolves to two separate phases (solution values of +/- 1) . Since all of the activity occurs on the boundary between the two phase regions, refinement is only necessary where gradients are large. We start with the entire solution at the finest resolution and de-refine as the phases coalesce.

There are two movies of these results:

The First Movie shows the first 21000 timesteps. (Just the finest level is shown, so that it's obvious what's being de-refined)

The problem was then restarted from a checkpoint file and run out to 50,000 coarsest-level timesteps. The solution time is then 500.0. The second Movie shows the result of a restart (everything after the first movie).

Also, here are some snapshots: at the initial time, after 1000 timesteps, after 10,000 timesteps, and after 50,000 timesteps:

Images courtesy Frank Alexander (LANL) and Dan Martin (LBNL).

Back to the Image Gallery