LAPACKMatrix.H File Reference

#include "REAL.H"
#include "LoHiSide.H"
#include <utility>
#include "BaseNamespaceHeader.H"
#include "BaseNamespaceFooter.H"

Include dependency graph for LAPACKMatrix.H:

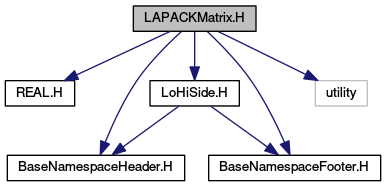
Go to the source code of this file.

Classes
class	LAPACKMatrix
Functions
Real	getInverseOfConditionNumber (const LAPACKMatrix &A)
void	multiply (LAPACKMatrix &a_product, const LAPACKMatrix &a_left, const LAPACKMatrix &a_right)
int	solveLeastSquares (LAPACKMatrix &A, LAPACKMatrix &B)
	below stuff is shamelessly stolen from lapackwrapper class
int	solveLeastSquaresTranspose (LAPACKMatrix &A, LAPACKMatrix &B)
int	solveLSTSVDOnce (LAPACKMatrix &X, const LAPACKMatrix &A, const LAPACKMatrix &B)
int	solveLSTSVD (LAPACKMatrix &A, LAPACKMatrix &B, int a_maxiter, Real a_tol)
int	solveEqualityConstrainedLS (LAPACKMatrix &A, LAPACKMatrix &c, LAPACKMatrix &B, LAPACKMatrix &d, LAPACKMatrix &x)
int	solveReducedRankLS (LAPACKMatrix &A, LAPACKMatrix &b)

---

Function Documentation

Real getInverseOfConditionNumber

(

const LAPACKMatrix &

A

)

Following Lapack, gets inverse of condition number. Returning a number near zero means the matrix is not really solvable.

void multiply	(	LAPACKMatrix &	a_product,
		const LAPACKMatrix &	a_left,
		const LAPACKMatrix &	a_right
	)

sets product = a_left* a_right fails if a_left.m_col != a_right.m_rows

int solveLeastSquares	(	LAPACKMatrix &	A,
		LAPACKMatrix &	B
	)

below stuff is shamelessly stolen from lapackwrapper class

Solves A*X = B using general least squares, for each column of B

int solveLeastSquaresTranspose	(	LAPACKMatrix &	A,
		LAPACKMatrix &	B
	)

Solves A'*X = B using least squares, for vector b

int solveLSTSVDOnce	(	LAPACKMatrix &	X,
		const LAPACKMatrix &	A,
		const LAPACKMatrix &	B
	)

Solves A*X = B using least squares with SVD, for X

int solveLSTSVD	(	LAPACKMatrix &	A,
		LAPACKMatrix &	B,
		int	a_maxiter,
		Real	a_tol
	)

Solves A^T X = B using least squares with SVD, for vector b

int solveEqualityConstrainedLS	(	LAPACKMatrix &	A,
		LAPACKMatrix &	c,
		LAPACKMatrix &	B,
		LAPACKMatrix &	d,
		LAPACKMatrix &	x
	)

Solves equality constrained least squares problem Find x, s.t. min norm(A x - c) with B x = d

int solveReducedRankLS	(	LAPACKMatrix &	A,
		LAPACKMatrix &	b
	)

Solves A'*X = B using reduced rank least squares, for vector b