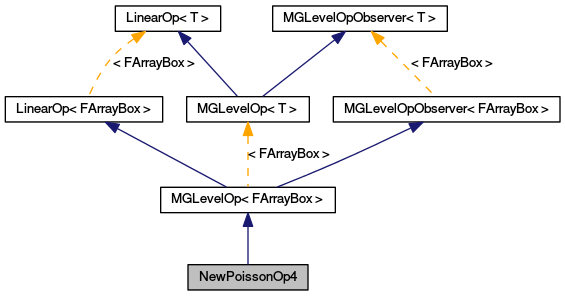
NewPoissonOp4 Class Reference
#include <NewPoissonOp4.H>
Public Member Functions | |
| NewPoissonOp4 () | |
| virtual | ~NewPoissonOp4 () |
LinearOp functions | |
| void | define (const RealVect &a_dx, const ProblemDomain &a_domain, BCFunc a_bc) |
| virtual void | createCoarsened (FArrayBox &a_lhs, const FArrayBox &a_rhs, const int &a_refRat) |
| virtual void | residual (FArrayBox &a_lhs, const FArrayBox &a_phi, const FArrayBox &a_rhs, bool a_homogeneous=false) |
| virtual void | preCond (FArrayBox &a_correction, const FArrayBox &a_residual) |
| virtual void | applyOp (FArrayBox &a_lhs, const FArrayBox &a_phi, bool a_homogeneous=false) |
| virtual void | create (FArrayBox &a_lhs, const FArrayBox &a_rhs) |
| virtual void | assign (FArrayBox &a_lhs, const FArrayBox &a_rhs) |
| virtual Real | dotProduct (const FArrayBox &a_1, const FArrayBox &a_2) |
| virtual void | incr (FArrayBox &a_lhs, const FArrayBox &a_x, Real a_scale) |
| virtual void | axby (FArrayBox &a_lhs, const FArrayBox &a_x, const FArrayBox &a_y, Real a, Real b) |
| virtual void | scale (FArrayBox &a_lhs, const Real &a_scale) |
| virtual Real | norm (const FArrayBox &a_x, int a_ord) |
| virtual void | setToZero (FArrayBox &a_x) |
MGLevelOp functions | |
| virtual void | relax (FArrayBox &a_e, const FArrayBox &a_residual, int iterations) |
| virtual void | createCoarser (FArrayBox &a_coarse, const FArrayBox &a_fine, bool ghost) |
| virtual void | restrictResidual (FArrayBox &a_resCoarse, FArrayBox &a_phiFine, const FArrayBox &a_rhsFine) |
| virtual void | prolongIncrement (FArrayBox &a_phiThisLevel, const FArrayBox &a_correctCoarse) |
Static Public Attributes | |
| static const int | m_nGhost = 2 |
Protected Member Functions | |
| void | levelGSRB (FArrayBox &a_e, const FArrayBox &a_residual) |
Protected Attributes | |
| RealVect | m_dx |
| RealVect | m_dxCrse |
| ProblemDomain | m_domain |
| BCFunc | m_bc |
Constructor & Destructor Documentation
| NewPoissonOp4::NewPoissonOp4 | ( | ) | [inline] |
| virtual NewPoissonOp4::~NewPoissonOp4 | ( | ) | [inline, virtual] |
Member Function Documentation
| void NewPoissonOp4::define | ( | const RealVect & | a_dx, | |
| const ProblemDomain & | a_domain, | |||
| BCFunc | a_bc | |||
| ) |
| virtual void NewPoissonOp4::createCoarsened | ( | FArrayBox & | a_lhs, | |
| const FArrayBox & | a_rhs, | |||
| const int & | a_refRat | |||
| ) | [virtual] |
| virtual void NewPoissonOp4::residual | ( | FArrayBox & | a_lhs, | |
| const FArrayBox & | a_phi, | |||
| const FArrayBox & | a_rhs, | |||
| bool | a_homogeneous = false | |||
| ) | [virtual] |
Say you are solving L(phi) = rhs. Make a_lhs = L(a_phi) - a_rhs. If a_homogeneous is true, evaluate the operator using homogeneous boundary conditions.
Implements LinearOp< FArrayBox >.
Given the current state of the residual the correction, apply your preconditioner to a_cor.
Implements LinearOp< FArrayBox >.
| virtual void NewPoissonOp4::applyOp | ( | FArrayBox & | a_lhs, | |
| const FArrayBox & | a_phi, | |||
| bool | a_homogeneous = false | |||
| ) | [virtual] |
In the context of solving L(phi) = rhs, set a_lhs = L(a_phi). If a_homogeneous is true, evaluate the operator using homogeneous boundary conditions.
Implements LinearOp< FArrayBox >.
Creat data holder a_lhs that mirrors a_rhs. You do not need to copy the data of a_rhs, just make a holder the same size.
Implements LinearOp< FArrayBox >.
Set a_lhs equal to a_rhs.
Implements LinearOp< FArrayBox >.
Compute and return the dot product of a_1 and a_2. In most contexts, this means return the sum over all data points of a_1*a_2.
Implements LinearOp< FArrayBox >.
| virtual void NewPoissonOp4::incr | ( | FArrayBox & | a_lhs, | |
| const FArrayBox & | a_x, | |||
| Real | a_scale | |||
| ) | [virtual] |
Increment by scaled amount (a_lhs += a_scale*a_x).
Implements LinearOp< FArrayBox >.
| virtual void NewPoissonOp4::axby | ( | FArrayBox & | a_lhs, | |
| const FArrayBox & | a_x, | |||
| const FArrayBox & | a_y, | |||
| Real | a_a, | |||
| Real | a_b | |||
| ) | [virtual] |
Set input to a scaled sum (a_lhs = a_a*a_x + a_b*a_y).
Implements LinearOp< FArrayBox >.
Multiply the input by a given scale (a_lhs *= a_scale).
Implements LinearOp< FArrayBox >.
Return the norm of a_rhs. a_ord == 0 max norm, a_ord == 1 sum(abs(a_rhs)), else, L(a_ord) norm.
Implements LinearOp< FArrayBox >.
| virtual void NewPoissonOp4::setToZero | ( | FArrayBox & | a_lhs | ) | [virtual] |
Set a_lhs to zero.
Implements LinearOp< FArrayBox >.
| virtual void NewPoissonOp4::relax | ( | FArrayBox & | a_correction, | |
| const FArrayBox & | a_residual, | |||
| int | a_iterations | |||
| ) | [virtual] |
Use your relaxation operator to remove the high frequency wave numbers from the correction so that it may be averaged to a coarser refinement. A point relaxtion scheme, for example takes the form a_correction -= lambda*(L(a_correction) - a_residual).
Implements MGLevelOp< FArrayBox >.
| virtual void NewPoissonOp4::createCoarser | ( | FArrayBox & | a_coarse, | |
| const FArrayBox & | a_fine, | |||
| bool | ghosted | |||
| ) | [virtual] |
Create a coarsened (by two) version of the input data. This does not include averaging the data. So if a_fine is over a Box of (0, 0, 0) (63, 63, 63), a_fine should be over a Box (0, 0, 0) (31, 31, 31).
Implements MGLevelOp< FArrayBox >.
| virtual void NewPoissonOp4::restrictResidual | ( | FArrayBox & | a_resCoarse, | |
| FArrayBox & | a_phiFine, | |||
| const FArrayBox & | a_rhsFine | |||
| ) | [virtual] |
calculate restricted residual a_resCoarse[2h] = I[h->2h] (rhsFine[h] - L[h](phiFine[h])
Implements MGLevelOp< FArrayBox >.
| virtual void NewPoissonOp4::prolongIncrement | ( | FArrayBox & | a_phiThisLevel, | |
| const FArrayBox & | a_correctCoarse | |||
| ) | [virtual] |
correct the fine solution based on coarse correction a_phiThisLevel += I[2h->h](a_correctCoarse)
Implements MGLevelOp< FArrayBox >.
Member Data Documentation
const int NewPoissonOp4::m_nGhost = 2 [static] |
RealVect NewPoissonOp4::m_dx [protected] |
RealVect NewPoissonOp4::m_dxCrse [protected] |
ProblemDomain NewPoissonOp4::m_domain [protected] |
BCFunc NewPoissonOp4::m_bc [protected] |
The documentation for this class was generated from the following file:
 1.5.5
1.5.5