ScalarFunction Class Reference

#include <ScalarFunction.H>

Inheritance diagram for ScalarFunction:

[legend]

List of all members.

---

Detailed Description

This base class represents a scalar function .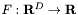

Public Member Functions
	ScalarFunction (bool a_homogeneous, bool a_constant)
virtual	~ScalarFunction ()
	Destructor.
virtual Real	operator() (const RealVect &a_x, Real a_t) const =0
virtual Real	derivative (const IntVect &a_order, const RealVect &a_x, Real a_t) const
virtual bool	hasDerivative (const IntVect &a_order) const
Real	operator() (const RealVect &a_x) const
Real	derivative (const IntVect &a_order, const RealVect &a_x) const
bool	isHomogeneous () const
	Returns true if this function is homogeneous, false otherwise.
bool	isConstant () const
	Returns true if this function is constant, false otherwise.
Protected Attributes
bool	m_isHomogeneous
bool	m_isConstant
Private Member Functions
	ScalarFunction ()
	ScalarFunction (const ScalarFunction &)
ScalarFunction &	operator= (const ScalarFunction &)

---

Constructor & Destructor Documentation

ScalarFunction::ScalarFunction	(	bool	a_homogeneous,
		bool	a_constant
	)

Base class constructor. Must be called by subclasses.

Parameters:

	a_homogeneous	This flag indicates whether the scalar function is constant in space.
	a_constant	This flag indicates whether the scalar function is constant in time.

virtual ScalarFunction::~ScalarFunction

(

)

[virtual]

Destructor.

ScalarFunction::ScalarFunction

(

)

[private]

ScalarFunction::ScalarFunction

(

const ScalarFunction &

)

[private]

---

Member Function Documentation

virtual Real ScalarFunction::operator()	(	const RealVect &	a_x,
		Real	a_t
	)			const [pure virtual]

Override this method to evaluate this function at the given point in space and time.

Parameters:

	a_x	A point in 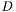-dimensional space.
	a_t	The time at which the function is to be evaluated.

Implemented in ConstantScalarFunction.

Referenced by operator()().

virtual Real ScalarFunction::derivative	(	const IntVect &	a_order,
		const RealVect &	a_x,
		Real	a_t
	)			const [virtual]

Override this method to evaluate the given partial derivative of the function at the given point in space and time.

Parameters:

	a_order	A multi-index identifying the order(s) of the partial derivative of the function to be evaluated.
	a_x	A point in 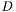-dimensional space.
	a_t	The time at which the derivative is to be evaluated.

Reimplemented in ConstantScalarFunction.

Referenced by derivative().

virtual bool ScalarFunction::hasDerivative

(

const IntVect &

a_order

)

const [virtual]

Override this method to return true if the derivative of the requested order exists and is available, false if it is not. This must be implemented in a way that is consistent with the derivative method.

Parameters:

a_order

A multi-index identifying the order(s) of the desired partial derivative of the function.

Real ScalarFunction::operator()

(

const RealVect &

a_x

)

const [inline]

This evaluates the function at time 0.

Parameters:

a_x

A point in 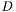-dimensional space.

References operator()().

Real ScalarFunction::derivative	(	const IntVect &	a_order,
		const RealVect &	a_x
	)			const [inline]

This evaluates the given partial derivative of the function at time 0.

Parameters:

	a_order	A multi-index identifying the order(s) of the partial derivative of the function to be evaluated.
	a_x	A point in 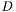-dimensional space.

References derivative().

bool ScalarFunction::isHomogeneous

(

)

const [inline]

Returns true if this function is homogeneous, false otherwise.

References m_isHomogeneous.

bool ScalarFunction::isConstant

(

)

const [inline]

Returns true if this function is constant, false otherwise.

References m_isConstant.

ScalarFunction& ScalarFunction::operator=

(

const ScalarFunction &

)

[private]

---

Member Data Documentation

bool ScalarFunction::m_isHomogeneous [protected]

Referenced by isHomogeneous().

bool ScalarFunction::m_isConstant [protected]

Referenced by isConstant().

---

The documentation for this class was generated from the following file:

• ScalarFunction.H