ScalarFunction Class Reference

#include <ScalarFunction.H>

Inheritance diagram for ScalarFunction:

Public Member Functions
	ScalarFunction (bool a_homogeneous, bool a_constant)
virtual	~ScalarFunction ()
	Destructor. More...
virtual Real	operator() (const RealVect &a_x, Real a_t) const =0
virtual Real	derivative (const IntVect &a_order, const RealVect &a_x, Real a_t) const
virtual bool	hasDerivative (const IntVect &a_order) const
Real	operator() (const RealVect &a_x) const
Real	derivative (const IntVect &a_order, const RealVect &a_x) const
bool	isHomogeneous () const
	Returns true if this function is homogeneous, false otherwise. More...
bool	isConstant () const
	Returns true if this function is constant, false otherwise. More...

Protected Attributes
bool	m_isHomogeneous
bool	m_isConstant

Private Member Functions
	ScalarFunction ()
	ScalarFunction (const ScalarFunction &)
ScalarFunction &	operator= (const ScalarFunction &)

Detailed Description

This base class represents a scalar function .

Constructor & Destructor Documentation

ScalarFunction() [1/3]

ScalarFunction::ScalarFunction	(	bool	a_homogeneous,
		bool	a_constant
	)

Base class constructor. Must be called by subclasses.

Parameters

a_homogeneous	This flag indicates whether the scalar function is constant in space.
a_constant	This flag indicates whether the scalar function is constant in time.

~ScalarFunction()

virtual ScalarFunction::~ScalarFunction ( )

virtual

Destructor.

ScalarFunction() [2/3]

ScalarFunction::ScalarFunction ( )

private

ScalarFunction() [3/3]

ScalarFunction::ScalarFunction ( const ScalarFunction &  )

private

Member Function Documentation

operator()() [1/2]

virtual Real ScalarFunction::operator() ( const RealVect &  a_x, Real  a_t  ) const

pure virtual

Override this method to evaluate this function at the given point in space and time.

Parameters

a_x	A point in 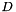-dimensional space.
a_t	The time at which the function is to be evaluated.

Implemented in ConstantScalarFunction.

Referenced by operator()().

derivative() [1/2]

virtual Real ScalarFunction::derivative ( const IntVect &  a_order, const RealVect &  a_x, Real  a_t  ) const

virtual

Override this method to evaluate the given partial derivative of the function at the given point in space and time.

Parameters

a_order	A multi-index identifying the order(s) of the partial derivative of the function to be evaluated.
a_x	A point in 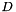-dimensional space.
a_t	The time at which the derivative is to be evaluated.

Reimplemented in ConstantScalarFunction.

Referenced by derivative().

hasDerivative()

virtual bool ScalarFunction::hasDerivative ( const IntVect &  a_order ) const

virtual

Override this method to return true if the derivative of the requested order exists and is available, false if it is not. This must be implemented in a way that is consistent with the derivative method.

Parameters

a_order

A multi-index identifying the order(s) of the desired partial derivative of the function.

operator()() [2/2]

Real ScalarFunction::operator() ( const RealVect &  a_x ) const

inline

This evaluates the function at time 0.

Parameters

a_x	A point in 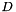-dimensional space.

References operator()().

derivative() [2/2]

Real ScalarFunction::derivative ( const IntVect &  a_order, const RealVect &  a_x  ) const

inline

This evaluates the given partial derivative of the function at time 0.

Parameters

a_order	A multi-index identifying the order(s) of the partial derivative of the function to be evaluated.
a_x	A point in 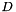-dimensional space.

References derivative().

isHomogeneous()

bool ScalarFunction::isHomogeneous ( ) const

inline

Returns true if this function is homogeneous, false otherwise.

References m_isHomogeneous.

isConstant()

bool ScalarFunction::isConstant ( ) const

inline

Returns true if this function is constant, false otherwise.

References m_isConstant.

operator=()

ScalarFunction& ScalarFunction::operator= ( const ScalarFunction &  )

private

Member Data Documentation

m_isHomogeneous

bool ScalarFunction::m_isHomogeneous

protected

Referenced by isHomogeneous().

m_isConstant

bool ScalarFunction::m_isConstant

protected

Referenced by isConstant().

---

The documentation for this class was generated from the following file:

• ScalarFunction.H