Chombo + EB + MF  3.2
Public Member Functions | Public Attributes | Protected Types | Protected Member Functions | Private Member Functions | List of all members
FourthOrderMappedFineInterp Class Reference

Interpolate from coarse cells to valid fine cells on mapped grids. More...

#include <FourthOrderMappedFineInterp.H>

Public Member Functions

 FourthOrderMappedFineInterp (const int a_degree, const int a_nComp)
 Non-defining construction. More...
 
 FourthOrderMappedFineInterp (const int a_degree, const int a_nComp, const IntVect &a_refRatio, const RealVect &a_h)
 Constructor that initializes the stencils. More...
 
 ~FourthOrderMappedFineInterp ()
 Destructor. More...
 
virtual void defineStencils (const IntVect &a_refRatio, const RealVect &a_h)
 Define that initializes the stencils. More...
 
virtual void defineGrids (const DisjointBoxLayout &a_FnGrid, const DisjointBoxLayout &a_CrGrid, const ProblemDomain &a_CrProblemDomain, const IntVect &a_FnInterpRadVec=IntVect::Zero, const bool a_willFillGhostsWithCrFnJU=true, const MultiBlockLevelGeom *const a_mbgeoPtr=0)
 Define that allocates data for coarse representations of the fine grid. More...
 
virtual void defineCrFnJ (const LevelData< FArrayBox > &a_CrJ)
 Define that saves the coarse <J> on the coarsened-fine layout. More...
 
virtual void defineCFInterface (LevelGridMetrics *const a_CrMetricsPtr)
 Define that initializes the coarse-fine interface for filling ghosts. More...
 
virtual void interpToFine (LevelData< FArrayBox > &a_FnLevJU, const LevelData< FArrayBox > &a_FnLevJ, const LevelData< FArrayBox > &a_CrLevU, const LevelData< FArrayBox > &a_CrLevJU, LevelGridMetrics *const a_CrMetricsPtr, const Interval &a_vectorIntv)
 Interpolate from a coarse to fine level on a mapped grid. More...
 
void fillGhosts (LevelData< FArrayBox > &a_FnLevU, LevelData< FArrayBox > &a_FnLevJU, const LevelData< FArrayBox > &a_FnLevJ, const LevelData< FArrayBox > &a_CrLevData, const char *const a_CrDataType, const ProblemDomain &a_CrProblemDomain)
 Fill the invalid ghost cells on a mapped grid. More...
 
virtual void fillGhosts (LevelData< FArrayBox > &a_FnLevU, LevelData< FArrayBox > &a_FnLevJU, const LevelData< FArrayBox > &a_FnLevJ, LevelGridMetrics *const a_CrMetricsPtr)
 Fill invalid ghost cells from preset coarsened-fine data on a mapped grid. More...
 
virtual void interpCrFnToFine (LevelData< FArrayBox > &a_FnLevJU, const LevelData< FArrayBox > &a_FnLevJ, const DisjointBoxLayout &a_CrFnGrid, const LevelData< FArrayBox > &a_CrFnLevU, const LevelData< FArrayBox > &a_CrFnLevJU, LevelGridMetrics *const a_CrMetricsPtr) const
 Interpolate from a coarsened-fine to fine level on a mapped grid. More...
 
int interpToFine (FArrayBox &a_FnFabJU, const FArrayBox &a_FnFabJ, const Box &a_CrBox, const FArrayBox &a_CrFabU, const FArrayBox &a_CrFabJU, const ProblemDomain &a_CrProblemDomain) const
 Interpolate from a coarse to fine box on a mapped grid. More...
 
void fillGhosts (FArrayBox &a_FnFabU, FArrayBox &a_FnFabJU, const FArrayBox &a_FnFabJ, const IntVectSet &a_CrCells, const BaseFab< int > &a_CrCellsArIdx, const FArrayBox &a_CrFabU, const ProblemDomain &a_CrProblemDomain) const
 Fill any ghost cells on a finer mesh. More...
 
bool isStencilDefined () const
 True if stencil defined. More...
 
bool isGridDefined () const
 True if coarsend-fine grid data defined. More...
 
bool isCFInterfaceDefined () const
 True if coarse-fine interface defined. More...
 
bool isCrFnJDefined () const
 True if coarse-fine <J> defined. More...
 
bool properNesting (const DisjointBoxLayout &a_CrBoxes, const DisjointBoxLayout &a_CrFnBoxes, LevelGridMetrics *const a_CrMetricsPtr) const
 Check for proper nesting of the fine level in the coarse level. More...
 
virtual LevelData< FArrayBox > & presetCrFnLevU ()
 Preset the coarsened-fine <U> externally. More...
 
virtual LevelData< FArrayBox > & presetCrFnLevJU ()
 Preset the coarsened-fine <JU> externally. More...
 
virtual void presetCrFnLevU (const LevelData< FArrayBox > &a_CrLevU, const Interval &a_vectorIntv)
 Preset the coarsened-fine <U> from coarse level data. More...
 
virtual void invalidateCrFnLevData ()
 Invalidate the CrFn data, both <U> and <JU> More...
 
const IntVect & CrFnNumGhost () const
 Get the number of ghosts used to build the coarsened-fine data. More...
 
int nComp () const
 Return the number of components. More...
 

Public Attributes

const int m_degree
 Degree of interpolating polynomial. More...
 
const int m_stencilExtent
 
const int m_nComp
 
IntVect m_refRatio
 Refinement ratios between the levels. More...
 
int m_numStencil
 Number of possible stencils. More...
 
int m_numUniqueDx
 
int m_uniqueDx [SpaceDim]
 
bool m_defined [4]
 
bool m_willFillGhostsWithCrFnJU
 
std::map< int, int > m_mapStencilIndex
 
CHArray< IntVectSet, 1 > m_ivsStencilMask
 Masks for the various stencils. More...
 
CHArray< CHMatrix, 1, ArZeroCol, ArSp::ArrayOfMatrixAlloc > m_At
 
CHArray< Real, SpaceDim+1, ArRangeCol > * m_fnXiLSx
 
CHArray< Real, SpaceDim+1, ArRangeCol > * m_fnGradXiLSx
 
CHArray< Real, SpaceDim+1, ArRangeCol > m_avgXipFine
 
CHArray< Real, SpaceDim+1, ArRangeCol > m_avgXiKpFine
 
CHArray< Real, SpaceDim+1, ArRangeCol > m_avgGradXipFine
 
DisjointBoxLayout m_CrFnGrid
 The coarsened-fine boxes. More...
 
LevelData< FArrayBox > m_CrFnLevU
 
LevelData< FArrayBox > m_CrFnLevJU
 
LevelData< FArrayBox > m_CrFnLevJ
 
Copier m_copier
 
MultiBlockLevelCopierAverage m_mbcp
 
IntVect m_FnInterpRadVec
 
IntVect m_CrInterpRadVec
 
IntVect m_CrFnNumGhost
 
LayoutData< IntVectSet > m_CrFnFillInterp
 
LayoutData< BaseFab< int > > m_ArIdxFillInterp
 
CHArray< Box, 1, ArZeroCol > m_FnBoxFillInterp
 
int m_numCrFnFillGhost
 
int m_CrFnStatus
 
bool m_isMultiblock
 T - A multiblock coordinates system. More...
 

Protected Types

enum  CrFnStatus { CrFnStatusInvalid = 0, CrFnStatusHaveJU = 1, CrFnStatusHaveU = 2 }
 Status of internal coarsened-fine data. More...
 

Protected Member Functions

bool isMultiblock () const
 Is this a multiblock grid. More...
 

Private Member Functions

 FourthOrderMappedFineInterp (const FourthOrderMappedFineInterp &)
 
FourthOrderMappedFineInterp & operator= (const FourthOrderMappedFineInterp &)
 
void selectStencil (const IntVect a_center, const ProblemDomain &a_CrProblemDomain, int &a_iStencil, CoordTransform &a_ctStoP, CoordTransform &a_ctPtoS, IntVect &a_offset, IntVect &a_fineSmlEnd) const
 
void sortEachSetDx (int *const a_a, int *const a_b) const
 Sort sets of dimensions with the same mesh spacing. More...
 
int offset2Key (const int *const a_offsets) const
 Get the stencil key from a list of offsets. More...
 
void loadAvgXipA (Real *a_A, const RealVect &a_dxi, const RealVect a_h) const
 Load 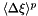$\langle \Delta\xi \rangle^p$ for all p. More...
 
void loadAvgXiKpA (Real *a_A, const RealVect &a_dxi, const RealVect a_h) const
 Load 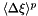$\langle \Delta\xi \rangle^p$ for all p, evaluated with K. More...
 
void loadAvgGradXip (Real *a_gradXip, const RealVect &a_dxi, const RealVect a_h) const
 Load gradients of 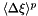$\langle \Delta\xi \rangle^p$ for all p. More...
 

Detailed Description

Interpolate from coarse cells to valid fine cells on mapped grids.

This class is used to interpolate the solution from coarse cells to valid fine cells on mapped grids using a constrained least-squares procedure. We solve a least-squares system for the coefficients of a polynomial interpolant

\[ \sum \limits_{\mathbf{p}} a_{\mathbf{p}} \langle \mathbf{\xi}^\mathbf{p} \rangle_{\mathbf{j}^l} = \langle U \rangle_{\mathbf{j}^l} \hbox{ , } \mathbf{j}^l \in \mathcal{I}(\mathbf{i}^l) \]

subject to the constraint

\[ \sum \limits_{\mathbf{i}^{l+1} \in \mathcal{C}^{-1} {\mathbf{i}^l }} \sum \limits_{\mathbf{p}} a_\mathbf{p} \langle J \mathbf{\xi}^\mathbf{p} \rangle_{\mathbf{i}^{l+1}} = \langle J U \rangle_{\mathbf{i}^l}. \]

Given this interpolant, we can construct 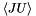$\langle JU \rangle$ on the control volumes at level $l+1$.

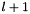\[ \langle JU \rangle_{\mathbf{i}^{l+1}} = \sum \limits_\mathbf{p} a_\mathbf{p} \langle J\mathbf{\xi}^\mathbf{p} \rangle_{\mathbf{i}^{l+1}} \hbox{ , } \mathbf{i}^{l+1} \in \mathcal{C}^{-1}(\mathbf{i}^{l}) \]

The details of the method are described in the Chombo document titled "Fourth-order conservation law example"

Implementation
To compute the coefficients, we solve the system

\[ \min_{{B \mathbf{x}} = \mathbf{d}} \| A \mathbf{x} - \mathbf{b} \|_2 \]

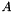where $A$ is the lenM x lenN coefficient matrix of 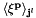$\langle \mathbf{\xi}^\mathbf{p} \rangle_{\mathbf{j}^l}$. lenM is the number of equations (number of cells in the stencil, the maximum value is for the interior stencil where 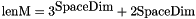$\mbox{lenM} = 3^{\mbox{SpaceDim}} + 2\mbox{SpaceDim}$ and lenN is the number of powers of a displacement given by 0 = binomial(degree + SpaceDim, SpaceDim) where degree is the order of interpolation (i.e., 3 for a cubic polynomial and fourth-order interpolation). 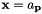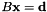We solve for coeffients $\mathbf{x} = a_\mathbf{p}$ where $B \mathbf{x} = \mathbf{d}$ is the constraint equation shown above. You will see this notation in the code, e.g, A, LSx, LSBu, LSbl, etc. Implementation is broken down into two parts. During construction, data is initialized that is valid for any boxes with the same mesh spacing and refinement ratios. Specifically, this is A and the displacements in the fine cells. Then, the member function, 'interpolate', will then interpolate everywhere on a coarse box.

The solution can be achieved using the LAPACK [S|D]GGLSE routine or an internal method which solves the linear system using a Cholesky factoriza- tion. Define statements in the Fortran routine 'maplsinterp' are used to select the method. The internal method is faster by a factor of about 4 for 2 components in the solution and should be even faster for more components. If both are used, the results are compared to some tolerance.

Stencil
The standard interior stencil has an inner box with size 3 and outer cells added in each dimension. See the Chombo doc mentioned above for more details and boundary stencils. The maximum stencil extent is shown below when cell 'i' is adjacent to the boundary. The encroachment of the wall in this example is by two cells relative to cell 'i' in the interior stencil. We label this as a "stencil offset from interior" of 2 in this direction, (2, 0). In this fashion, we can mark all the possible stencils. 

*           +---+                                   +---+\\
*           |   |                                   |   |\\
*       +===========+                       +===========+\\
*       H   |   |   H                       H   |   |   H\\
*   +---H---+---+---H---+               +---H---+---+---H\\
*   |   H   | i |   H   |               |   H   |   | i H\\
*   +---H---+---+---H---+               +---H---+---+---H\\
*       H   |   |   H                       H   |   |   H\\
*       +===========+                       +===========+\\
*           |   |                                   |   |\\
*           +---+                                   +---+\\
*              <---2--> stencil extent    <-----3----> max stencil extent
*

The stencils along with the coefficient matrices are stored during construction. To minimize the required memory, symmetric stencils are only stored once and coordinate transformations are used during actual interpolation. In the above example, a wall on the left would produce an identical but reflected stencil. If dx = dy, then walls on the top and bottom would also form the same stencil with some rotational similarity. Without any symmetry, the number of required stencils is given by 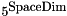$5^{\mbox{SpaceDim}}$. By exploiting symmetry in a given direction (quadrant), the number of stencils is 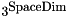$3^{\mbox{SpaceDim}}$. By exploiting symmetry between directions with the same mesh spacing, the number of stencils is binomial(SpaceDim + 2, 2). This has a dramatic effect at higher dimensions. At 6 dimensions, the memory required for 64 bit storage of matrix A are 7.246 GiB, 346 MiB, and 13 MiB, respectively. For 3 dimensions, this is 644 KiB, 139 KiB, and 52 KiB, respectively. All possible symmetries are exploited herein, both within a direction and between directions with the same mesh spacing.

Note
  • Most of the hard-core work is written in Fortran in file FourthOrderMappedFineInerpF.ChF.
  • loadAvgXipA is written in both C++ and Fortran exploring ways of using the SpaceDim macros. Both seem to have similar performance.
  • The min box size in any given direction is 4. 11/24/10 I don't think this is true – proper nesting is all that is required.

Member Enumeration Documentation

◆ CrFnStatus

enum FourthOrderMappedFineInterp::CrFnStatus
protected

Status of internal coarsened-fine data.

Enumerator
CrFnStatusInvalid 
CrFnStatusHaveJU 
CrFnStatusHaveU 

Constructor & Destructor Documentation

◆ FourthOrderMappedFineInterp() [1/3]

FourthOrderMappedFineInterp::FourthOrderMappedFineInterp ( const int  a_degree,
const int  a_nComp 
)

Non-defining construction.

◆ FourthOrderMappedFineInterp() [2/3]

FourthOrderMappedFineInterp::FourthOrderMappedFineInterp ( const int  a_degree,
const int  a_nComp,
const IntVect &  a_refRatio,
const RealVect &  a_h 
)

Constructor that initializes the stencils.

◆ ~FourthOrderMappedFineInterp()

FourthOrderMappedFineInterp::~FourthOrderMappedFineInterp ( )

Destructor.

◆ FourthOrderMappedFineInterp() [3/3]

FourthOrderMappedFineInterp::FourthOrderMappedFineInterp ( const FourthOrderMappedFineInterp &  )
private

Member Function Documentation

◆ operator=()

FourthOrderMappedFineInterp& FourthOrderMappedFineInterp::operator= ( const FourthOrderMappedFineInterp &  )
private

◆ defineStencils()

virtual void FourthOrderMappedFineInterp::defineStencils ( const IntVect &  a_refRatio,
const RealVect &  a_h 
)
virtual

Define that initializes the stencils.

◆ defineGrids()

virtual void FourthOrderMappedFineInterp::defineGrids ( const DisjointBoxLayout &  a_FnGrid,
const DisjointBoxLayout &  a_CrGrid,
const ProblemDomain &  a_CrProblemDomain,
const IntVect &  a_FnInterpRadVec = IntVect::Zero,
const bool  a_willFillGhostsWithCrFnJU = true,
const MultiBlockLevelGeom *const  a_mbgeoPtr = 0 
)
virtual

Define that allocates data for coarse representations of the fine grid.

◆ defineCrFnJ()

virtual void FourthOrderMappedFineInterp::defineCrFnJ ( const LevelData< FArrayBox > &  a_CrJ)
virtual

Define that saves the coarse <J> on the coarsened-fine layout.

◆ defineCFInterface()

virtual void FourthOrderMappedFineInterp::defineCFInterface ( LevelGridMetrics *const  a_CrMetricsPtr)
virtual

Define that initializes the coarse-fine interface for filling ghosts.

◆ interpToFine() [1/2]

virtual void FourthOrderMappedFineInterp::interpToFine ( LevelData< FArrayBox > &  a_FnLevJU,
const LevelData< FArrayBox > &  a_FnLevJ,
const LevelData< FArrayBox > &  a_CrLevU,
const LevelData< FArrayBox > &  a_CrLevJU,
LevelGridMetrics *const  a_CrMetricsPtr,
const Interval &  a_vectorIntv 
)
virtual

Interpolate from a coarse to fine level on a mapped grid.

◆ fillGhosts() [1/3]

void FourthOrderMappedFineInterp::fillGhosts ( LevelData< FArrayBox > &  a_FnLevU,
LevelData< FArrayBox > &  a_FnLevJU,
const LevelData< FArrayBox > &  a_FnLevJ,
const LevelData< FArrayBox > &  a_CrLevData,
const char *const  a_CrDataType,
const ProblemDomain &  a_CrProblemDomain 
)

Fill the invalid ghost cells on a mapped grid.

◆ fillGhosts() [2/3]

virtual void FourthOrderMappedFineInterp::fillGhosts ( LevelData< FArrayBox > &  a_FnLevU,
LevelData< FArrayBox > &  a_FnLevJU,
const LevelData< FArrayBox > &  a_FnLevJ,
LevelGridMetrics *const  a_CrMetricsPtr 
)
virtual

Fill invalid ghost cells from preset coarsened-fine data on a mapped grid.

◆ interpCrFnToFine()

virtual void FourthOrderMappedFineInterp::interpCrFnToFine ( LevelData< FArrayBox > &  a_FnLevJU,
const LevelData< FArrayBox > &  a_FnLevJ,
const DisjointBoxLayout &  a_CrFnGrid,
const LevelData< FArrayBox > &  a_CrFnLevU,
const LevelData< FArrayBox > &  a_CrFnLevJU,
LevelGridMetrics *const  a_CrMetricsPtr 
) const
virtual

Interpolate from a coarsened-fine to fine level on a mapped grid.

◆ interpToFine() [2/2]

int FourthOrderMappedFineInterp::interpToFine ( FArrayBox &  a_FnFabJU,
const FArrayBox &  a_FnFabJ,
const Box &  a_CrBox,
const FArrayBox &  a_CrFabU,
const FArrayBox &  a_CrFabJU,
const ProblemDomain &  a_CrProblemDomain 
) const

Interpolate from a coarse to fine box on a mapped grid.

◆ fillGhosts() [3/3]

void FourthOrderMappedFineInterp::fillGhosts ( FArrayBox &  a_FnFabU,
FArrayBox &  a_FnFabJU,
const FArrayBox &  a_FnFabJ,
const IntVectSet &  a_CrCells,
const BaseFab< int > &  a_CrCellsArIdx,
const FArrayBox &  a_CrFabU,
const ProblemDomain &  a_CrProblemDomain 
) const

Fill any ghost cells on a finer mesh.

◆ isStencilDefined()

bool FourthOrderMappedFineInterp::isStencilDefined ( ) const
inline

True if stencil defined.

Returns
T - stencil has been defined

References m_defined.

◆ isGridDefined()

bool FourthOrderMappedFineInterp::isGridDefined ( ) const
inline

True if coarsend-fine grid data defined.

Returns
T - coarsend-fine grid data has been defined

References m_defined.

Referenced by CrFnNumGhost(), presetCrFnLevJU(), and presetCrFnLevU().

◆ isCFInterfaceDefined()

bool FourthOrderMappedFineInterp::isCFInterfaceDefined ( ) const
inline

True if coarse-fine interface defined.

Returns
T - coarse-fine interface has been defined

References m_defined.

◆ isCrFnJDefined()

bool FourthOrderMappedFineInterp::isCrFnJDefined ( ) const
inline

True if coarse-fine <J> defined.

Must be defined to fill ghosts using 'fillGhostsFromCrJU'

Returns
T - m_CrFnLevJ has been defined

References m_defined.

◆ properNesting()

bool FourthOrderMappedFineInterp::properNesting ( const DisjointBoxLayout &  a_CrBoxes,
const DisjointBoxLayout &  a_CrFnBoxes,
LevelGridMetrics *const  a_CrMetricsPtr 
) const

Check for proper nesting of the fine level in the coarse level.

◆ presetCrFnLevU() [1/2]

LevelData< FArrayBox > & FourthOrderMappedFineInterp::presetCrFnLevU ( )
inlinevirtual

Preset the coarsened-fine <U> externally.

This returns the coarsened-fine representation and you have to do the copyTo externally

References CH_assert, CrFnStatusHaveU, isGridDefined(), m_CrFnLevU, and m_CrFnStatus.

◆ presetCrFnLevJU()

LevelData< FArrayBox > & FourthOrderMappedFineInterp::presetCrFnLevJU ( )
inlinevirtual

Preset the coarsened-fine <JU> externally.

This returns the coarsened-fine representation and you have to do the copyTo externally

References CH_assert, CrFnStatusHaveJU, isGridDefined(), m_CrFnLevJU, and m_CrFnStatus.

◆ presetCrFnLevU() [2/2]

virtual void FourthOrderMappedFineInterp::presetCrFnLevU ( const LevelData< FArrayBox > &  a_CrLevU,
const Interval &  a_vectorIntv 
)
virtual

Preset the coarsened-fine <U> from coarse level data.

◆ invalidateCrFnLevData()

void FourthOrderMappedFineInterp::invalidateCrFnLevData ( )
inlinevirtual

Invalidate the CrFn data, both <U> and <JU>

References CrFnStatusInvalid, and m_CrFnStatus.

◆ CrFnNumGhost()

const IntVect & FourthOrderMappedFineInterp::CrFnNumGhost ( ) const
inline

Get the number of ghosts used to build the coarsened-fine data.

References CH_assert, isGridDefined(), and m_CrFnNumGhost.

◆ nComp()

int FourthOrderMappedFineInterp::nComp ( ) const
inline

Return the number of components.

References m_nComp.

◆ selectStencil()

void FourthOrderMappedFineInterp::selectStencil ( const IntVect  a_center,
const ProblemDomain &  a_CrProblemDomain,
int &  a_iStencil,
CoordTransform &  a_ctStoP,
CoordTransform &  a_ctPtoS,
IntVect &  a_offset,
IntVect &  a_fineSmlEnd 
) const
private

◆ sortEachSetDx()

void FourthOrderMappedFineInterp::sortEachSetDx ( int *const  a_a,
int *const  a_b 
) const
private

Sort sets of dimensions with the same mesh spacing.

◆ offset2Key()

int FourthOrderMappedFineInterp::offset2Key ( const int *const  a_offsets) const
private

Get the stencil key from a list of offsets.

◆ loadAvgXipA()

void FourthOrderMappedFineInterp::loadAvgXipA ( Real *  a_A,
const RealVect &  a_dxi,
const RealVect  a_h 
) const
private

Load 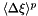$\langle \Delta\xi \rangle^p$ for all p.

◆ loadAvgXiKpA()

void FourthOrderMappedFineInterp::loadAvgXiKpA ( Real *  a_A,
const RealVect &  a_dxi,
const RealVect  a_h 
) const
private

Load 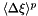$\langle \Delta\xi \rangle^p$ for all p, evaluated with K.

◆ loadAvgGradXip()

void FourthOrderMappedFineInterp::loadAvgGradXip ( Real *  a_gradXip,
const RealVect &  a_dxi,
const RealVect  a_h 
) const
private

Load gradients of 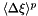$\langle \Delta\xi \rangle^p$ for all p.

◆ isMultiblock()

bool FourthOrderMappedFineInterp::isMultiblock ( ) const
inlineprotected

Is this a multiblock grid.

Returns
T - Yes

References m_isMultiblock.

Member Data Documentation

◆ m_degree

const int FourthOrderMappedFineInterp::m_degree

Degree of interpolating polynomial.

◆ m_stencilExtent

const int FourthOrderMappedFineInterp::m_stencilExtent

Maximum extent of interior stencil. Hard coded as 2.

◆ m_nComp

const int FourthOrderMappedFineInterp::m_nComp

Number of components for <U> and <JU>

Referenced by nComp().

◆ m_refRatio

IntVect FourthOrderMappedFineInterp::m_refRatio

Refinement ratios between the levels.

◆ m_numStencil

int FourthOrderMappedFineInterp::m_numStencil

Number of possible stencils.

◆ m_numUniqueDx

int FourthOrderMappedFineInterp::m_numUniqueDx

Number of different mesh spacing over all dimensions

◆ m_uniqueDx

int FourthOrderMappedFineInterp::m_uniqueDx[SpaceDim]

Marks sets of dimensions with the same mesh spacing

◆ m_defined

bool FourthOrderMappedFineInterp::m_defined[4]

0 - stencil, 1 - grids, 2 - CF interface, 3 - coarsened-fine<J>

Referenced by isCFInterfaceDefined(), isCrFnJDefined(), isGridDefined(), and isStencilDefined().

◆ m_willFillGhostsWithCrFnJU

bool FourthOrderMappedFineInterp::m_willFillGhostsWithCrFnJU

T - expecting to fill ghosts from from a coarsened-fine <JU> as specified in defineGrids().

◆ m_mapStencilIndex

std::map<int, int> FourthOrderMappedFineInterp::m_mapStencilIndex

Maps a key based on the stencil offset to a sequential index for a stencil

◆ m_ivsStencilMask

CHArray<IntVectSet, 1> FourthOrderMappedFineInterp::m_ivsStencilMask

Masks for the various stencils.

◆ m_At

CHArray<CHMatrix, 1, ArZeroCol, ArSp::ArrayOfMatrixAlloc> FourthOrderMappedFineInterp::m_At

The transpose of matrix A for solving 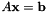$A\mathbf{x} = \mathbf{b}$. I.e., the powers of the displacements 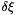$\delta\xi$ to the neighbour cells. The 'm_At' for all stencils are stored in a continguous chunk of memory by the ArrayOfMatrixAlloc allocator

◆ m_fnXiLSx

CHArray<Real, SpaceDim+1, ArRangeCol>* FourthOrderMappedFineInterp::m_fnXiLSx

Fine displacements already multiplied by the solution to the constrained least-squares problem (LSx). Multiply by LSbl to get <U> in a fine cell.

◆ m_fnGradXiLSx

CHArray<Real, SpaceDim+1, ArRangeCol>* FourthOrderMappedFineInterp::m_fnGradXiLSx

Gradients of fine displacements already multiplied by the solution to the constrained least-squares problem (LSx). Multiply by LSbl to get the gradient of <U> in a fine cell.

◆ m_avgXipFine

CHArray<Real, SpaceDim+1, ArRangeCol> FourthOrderMappedFineInterp::m_avgXipFine

Powers of displacements for fine cells

◆ m_avgXiKpFine

CHArray<Real, SpaceDim+1, ArRangeCol> FourthOrderMappedFineInterp::m_avgXiKpFine

Powers of displacements for fine cells with constant added to impose constraint when filling ghosts

◆ m_avgGradXipFine

CHArray<Real, SpaceDim+1, ArRangeCol> FourthOrderMappedFineInterp::m_avgGradXipFine

Gradients of 'm_avgXipFine'. This is stored linearly in each cell as (SpaceDim, p) with 'p' contiguous since fortran only supports rank 7 arrays (at least until F2008 becomes commonplace).

◆ m_CrFnGrid

DisjointBoxLayout FourthOrderMappedFineInterp::m_CrFnGrid

The coarsened-fine boxes.

◆ m_CrFnLevU

LevelData<FArrayBox> FourthOrderMappedFineInterp::m_CrFnLevU

<U> on a coarse representation of the fine mesh

Referenced by presetCrFnLevU().

◆ m_CrFnLevJU

LevelData<FArrayBox> FourthOrderMappedFineInterp::m_CrFnLevJU

<JU> on a coarse representation of the fine mesh

Referenced by presetCrFnLevJU().

◆ m_CrFnLevJ

LevelData<FArrayBox> FourthOrderMappedFineInterp::m_CrFnLevJ

<J> on a coarse representation of the fine mesh

◆ m_copier

Copier FourthOrderMappedFineInterp::m_copier

Friendly neighbourhood copier for copying from Cr to CrFn

◆ m_mbcp

MultiBlockLevelCopierAverage FourthOrderMappedFineInterp::m_mbcp

To copy information between diffferent layout across multiblock boundaries

◆ m_FnInterpRadVec

IntVect FourthOrderMappedFineInterp::m_FnInterpRadVec

Number of fine ghost cells that must be filled in each direction.

◆ m_CrInterpRadVec

IntVect FourthOrderMappedFineInterp::m_CrInterpRadVec

Number of coarse cells that underlie fine ghost cells in each direction

◆ m_CrFnNumGhost

IntVect FourthOrderMappedFineInterp::m_CrFnNumGhost

Number of layers of ghost cells required on the coarsened-fine mesh

Referenced by CrFnNumGhost().

◆ m_CrFnFillInterp

LayoutData<IntVectSet> FourthOrderMappedFineInterp::m_CrFnFillInterp

Coarse cells in which to interpolate to fill fine ghost cells

◆ m_ArIdxFillInterp

LayoutData<BaseFab<int> > FourthOrderMappedFineInterp::m_ArIdxFillInterp

Index into all the CHArray for an IntVect

◆ m_FnBoxFillInterp

CHArray<Box, 1, ArZeroCol> FourthOrderMappedFineInterp::m_FnBoxFillInterp

Box describing the fine cells that need to be filled in a coarse cell. Max size is n_{ref}^{l}

◆ m_numCrFnFillGhost

int FourthOrderMappedFineInterp::m_numCrFnFillGhost

Total number of coarse cells used to fill fine ghost cells on this processor (this is actually a count of total cells, not layers like numGhost usually is)

◆ m_CrFnStatus

int FourthOrderMappedFineInterp::m_CrFnStatus

Status of coarsened-fine data. We may know JU, U, or nothing. This is kept consistent with what MappedLevelData knows about the coarser data

Referenced by invalidateCrFnLevData(), presetCrFnLevJU(), and presetCrFnLevU().

◆ m_isMultiblock

bool FourthOrderMappedFineInterp::m_isMultiblock

T - A multiblock coordinates system.

Referenced by isMultiblock().

The documentation for this class was generated from the following file:
Generated by   doxygen 1.8.13