Grid metrics for a level. More...
#include <LevelGridMetrics.H>
Public Types | |
| enum | AgeType { AgeOld = 0, AgeNew = 1, AgeNum = 2 } |
| Age of metric terms during a regrid. More... | |
| enum | TransverseNOpType { TransverseNOpNone, TransverseNOpAnalytic, TransverseNOpAverage } |
| Type of operation for computing transverse terms in N. More... | |
Public Member Functions | |
| LevelGridMetrics (const int a_nComp, const int a_spaceOrder) | |
| Constructor. More... | |
| virtual | ~LevelGridMetrics () |
| Destructor. More... | |
| void | clear () |
| Free memory. More... | |
| bool | hasFiner () const |
| Does a finer level exist? More... | |
| bool | hasCoarser () const |
| Does a coarser level exist? More... | |
| void | define (AMRLevel *const a_AMRLevel, MultiBlockCoordSysFactory *const a_coordSysFact, LevelGridMetrics *const a_coarserLevelGridMetrics, const RealVect &a_dxVect, const IntVect &a_ghostVect, const TransverseNOpType a_transverseNOpType=TransverseNOpNone, const bool a_haveMultiBlockVectorData=true, const int a_numBlocks=1) |
| Define the class. No metrics terms are yet available. More... | |
| void | define (AMRLevel *const a_AMRLevel, MultiBlockCoordSys *const a_coordSys, LevelGridMetrics *const a_coarserLevelGridMetrics, const RealVect &a_dxVect, const IntVect &a_ghostVect, const TransverseNOpType a_transverseNOpType=TransverseNOpNone, const bool a_haveMultiBlockVectorData=true, const int a_numBlocks=1) |
| Define the class. No metrics terms are yet available. More... | |
| bool | metricsDefined () const |
| Are the metrics defined on this level? More... | |
| bool | didFinerChange () const |
| Did the metrics change on the finer mesh? More... | |
| const MultiBlockCoordSys & | getCoordSys () const |
| Retrieve the multi-block coordinate system. More... | |
| const NewCoordSys * | getCoordSys2 (const Box &box) const |
| Get the coordinate system. More... | |
| const NewFourthOrderCoordSys * | getCoordSys (const Box &box) const |
| int | getBlock (const Box &a_box) const |
| Get the block index. More... | |
| const ProblemDomain & | blockDomain (const Box &a_box, const int a_numGhost=0) |
| Get a problem domain representing a block. More... | |
| const RealVect & | dxVect () const |
| Get the computational mesh spacing. More... | |
| void | postTimeStep () |
After a time step, average down 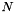 and and 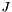 . More... . More... | |
| virtual void | initialGrid (const DisjointBoxLayout *const a_newGrid) |
| Set up initial grid. More... | |
| void | postInitialGrid (const DisjointBoxLayout *const a_newGrid) |
| Set up the initial metric terms. More... | |
| void | preRegrid (const int a_baseLevel, const DisjointBoxLayout &a_newGrid, const LevelData< FArrayBox > *const a_coarseUOldPtr, LevelData< FArrayBox > &a_UOld, LevelData< FArrayBox > &a_JUOld) |
| Compute new metrics and correct the solution on the coarser meshes. More... | |
| virtual void | regrid (LevelData< FArrayBox > &a_JU, const LevelData< FArrayBox > &a_CrU, const LevelData< FArrayBox > &a_CrJU, const Interval &a_vectorIntv) |
| Regrid operations – performs a coarse to fine interpolation. More... | |
| virtual void | fillFineGhostCells (LevelData< FArrayBox > &a_U, LevelData< FArrayBox > &a_JU, Real a_time=-1) |
| Fill invalid fine ghost cells (with preset CrFnU) More... | |
| void | computeValidU (LevelData< FArrayBox > &a_U, const LevelData< FArrayBox > &a_JU) |
| Computes <U> in valid cells. More... | |
| void | multiblockExchangeU (LevelData< FArrayBox > &a_U, const Interval &a_vectorIntv) const |
| Exchange <U> across multiblock boundaries. More... | |
| void | timeIntermediate (const TimeInterpolatorRK4 &a_timeInterpolator, const Real &a_timeInterpCoeff, const int &a_stage, const Interval &a_vectorIntv) |
| Supports a call to TimeInterpolatorRK4::intermediate for multi-block grids. More... | |
| LevelData< FArrayBox > & | presetCr2ThisInterpolatorCrFnLevU () |
| Set the coarsened-fine <U> used by the interpolator (CrFn access) More... | |
| LevelData< FArrayBox > & | presetCr2ThisInterpolatorCrFnLevJU () |
| Set the coarsened-fine <JU> used by the interpolator (CrFn access) More... | |
| void | presetThis2FnInterpolatorCrFnLevU (const LevelData< FArrayBox > &a_CrLevU, const Interval &a_vectorIntv) |
| Set the coarsened-fine <U> used by the interpolator. More... | |
| void | invalidateCr2ThisInterpolatorCrFnLevData () |
| Invalidate the CrFn data, both <U> and <JU>\, used by the interpolator. More... | |
| void | invalidateThis2FnInterpolatorCrFnLevData () |
| Invalidate the CrFn data, both <U> and <JU>\, used by the interpolator. More... | |
| const IntVect & | interpolatorCrFnNumGhost (const bool a_force=false) const |
| Number of ghosts used to build the coarsened-fine data in the interpolator. More... | |
| bool | isMultiblock () const |
| Is this a multiblock grid. More... | |
Consistent access to structural boxes | |
There are several places to get the boxes and interators from but all should be the same. These functions provide consistent access with sizes relevant to the metrics. | |
| const DisjointBoxLayout & | getBoxes () const |
| Get the boxes. More... | |
| DataIterator | getDataIterator () const |
| Get a level iterator. More... | |
| Box | resizeWithGhosts (const Box &box) const |
| Resize a box to include the ghost cells. More... | |
| virtual IntVect | getJReqGhostVect () const |
Determine the ghost vector required for 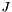 . More... . More... | |
| virtual IntVect | getNReqGhostVect () const |
Determine the ghost vector required for 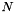 . More... . More... | |
| Box | resizeWithJReqGhosts (const Box &box) const |
Resize a box to the size required for 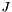 . More... . More... | |
| Box | resizeWithNReqGhosts (const Box &box) const |
Resize a box to the size required for 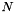 . More... . More... | |
Static Public Member Functions | |
| static int | bufferSize4thO (const std::vector< int > &a_refRatio, const int a_maxLevel, const int a_numGhost) |
| Compute the minimum grid buffer size for a fourth-order interpolation. More... | |
Public Attributes | |
| LevelData< FluxBox > | m_N |
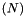 on each face More... on each face More... | |
| LevelData< FArrayBox > | m_J |
Protected Member Functions | |
| void | defineMetrics () |
| Completely define the metrics for this level. More... | |
| void | undefineMetrics () |
| Label this and all finer levels as having undefined metrics. More... | |
| void | faceNormalN (LevelData< FluxBox > &a_N, const LevelData< CodimBox< FArrayBox > > &a_scrN) |
Compute 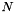 on the hyperfaces from on the hyperfaces from 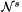 . More... . More... | |
| void | getN (LevelData< FluxBox > &a_N) |
Compute 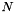 on the hyperfaces from on the hyperfaces from 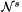 . More... . More... | |
| void | faceTransverseN (LevelData< FluxBox > &a_N) |
Add transverse components to 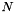 . More... . More... | |
| void | getScriptN (LevelData< CodimBox< FArrayBox > > &a_scrN) |
Integrate 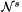 on each hyperedge. More... on each hyperedge. More... | |
| void | averageScriptN (const bool a_isBase, LevelData< CodimBox< FArrayBox > > &a_scrN) |
Average 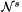 . More... . More... | |
| void | averageN (const bool a_isBase, LevelData< FluxBox > &a_N) |
Average 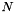 directly if directly if 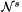 doesn't exist. More... doesn't exist. More... | |
| void | getVolFlux (LevelData< FluxBox > &a_NtX, const LevelData< FluxBox > &a_N) |
| Compute the volume flux. More... | |
| virtual void | setAvgJfromNtX (LevelData< FluxBox > &a_NtX) |
Take divergence of 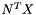 to set m_J. More... to set m_J. More... | |
| void | averageVolFlux (const bool a_isBase, LevelData< FluxBox > &a_NtX, const AgeType a_age) |
Average the volume flux 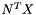 . More... . More... | |
| void | volFluxCascade () |
Compute 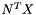 on all finer levels and average down. More... on all finer levels and average down. More... | |
| void | averageSnapbackSolFlux (const bool a_isBase, LevelData< FluxBox > &a_NtFDiff) |
Average the snapback solution flux, 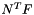 . More... . More... | |
| virtual void | defineGrids (const DisjointBoxLayout &a_grids) |
| Store the DisjointBoxLayout and define multiblock structures. More... | |
| void | defineGridsNP (const DisjointBoxLayout &a_grids) |
| Create a non-periodic DisjointBoxLayout. More... | |
Static Protected Member Functions | |
| static int | verbosity () |
Static Protected Attributes | |
| static int | s_verbosity |
Private Member Functions | |
| LevelGridMetrics (const LevelGridMetrics &) | |
| LevelGridMetrics & | operator= (const LevelGridMetrics &) |
Easier access to AMRLevel data | |
| const ProblemDomain & | problemDomain () const |
| int | level () const |
| int | refRatio () const |
Detailed Description
Grid metrics for a level.
This class adds infrastructure for mapped grids to the fourth-order Cartesian AMRLevel class. The interface closely follows that of AMRLevel. Typically this class is a member of the user's derived AMRLevel and the member functions of LevelGridData should be called from member functions of the derived AMRLevel that have the same name.
This class provides m_N, the metric terms 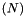 on each face, and m_J, the determinant (physical cell volume divided by computational cell volume). These quantities are appropriately maintained during all aspects of an AMR solution.
on each face, and m_J, the determinant (physical cell volume divided by computational cell volume). These quantities are appropriately maintained during all aspects of an AMR solution.
GHOSTS — The determinants, (J), are defined on all ghost cells at the domain interior and 1 layer of ghost cells outside a non-periodic domain. Hence, gradients of J are available everywhere an application may store data. To achieve this, it is assumed that the metrics can be evaluated everywhere in 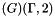 . HOWEVER, metrics that are consistent between levels are only maintained in the valid region of the finer level. A valid cell on a coarse level will have metrics computed separately from any overlapping ghost cells from a finer level (i.e., the volumes of the fine ghost cells may not sum to the volume of the valid coarse cell). Consistency between levels everywhere could be achieved by treating all ghost cells as part of the valid region — this would simply (probably simply) require some modifications to the "averagers". However we do not do this because:
. HOWEVER, metrics that are consistent between levels are only maintained in the valid region of the finer level. A valid cell on a coarse level will have metrics computed separately from any overlapping ghost cells from a finer level (i.e., the volumes of the fine ghost cells may not sum to the volume of the valid coarse cell). Consistency between levels everywhere could be achieved by treating all ghost cells as part of the valid region — this would simply (probably simply) require some modifications to the "averagers". However we do not do this because:
- it breaks a consistent definition of valid/invalid
- there is no requirement for conservation in ghost cells since they are only used for gradient reconstruction, limiting, etc.
Any ghost cell that is covered by a valid cell on that level is consistent with the metrics from any finer level by means of the copiers (used in the averagers) copying to both the invalid and valid regions of a destination.
Transverse terms in N are determined only on the faces of grow(N.box(), -1) if obtained by averaging, i.e., on one less layer than where the normal components are known. If obtained by analytic methods, they are available everywhere.
Normally, N is calculated using script N to ensure freestream preservation. But in some cases, e.g., a 2-D solution on the surface of a sphere, there is no definition of script N. In those cases, m_useScriptN should be set to false and N will be calculated and averaged directly. The averaging ensures conservation but freestream-preservation is sacrificed. The value of m_useScriptN is obtained from the MultiBlockCoordSys and should be set to 'false' in the constructor of coordinate systems derived from class MultiBlockCoordSys. Otherwise, by default, it is set to true.
The following routines should be called from the corresponding routines with the same name derived AMRLevel:
- initialGrid
- postInitialGrid
- postTimeStep
- preRegrid
- regrid
Setup for the class is as follows:
- Call define to setup the class members – metrics are still undefined.
- Optionally call initialGrid to set the new box layout on a level. This can be deferred until postInitialGrid if desired.
- Call postInitialGrid to set the new box layout (if not done in previous step) and define the metrics.
During a run, be sure to:
- Call postTimeStep to average down the metric terms from finer levels. This only has an effect if they changed on the finer level
For a regrid do the following:
- Call preRegrid to compute the new metrics and correct the solution on the old mesh to the metrics of the new mesh (snapback).
- Optionally call regrid to interpolate from the coarse mesh to the new fine mesh. This can be done is user code but must use FourthOrderMappedFineInterp to ensure a conservative and free-stream preserving interpolation on the mapped grid.
- Note
- To facilitate products that involve gradients, the metrics (N) are determined on the faces of boxes with size ghostBox+2. This is labeled an 'NReqGhostBox' herein. At domain boundaries, the boxes for 'N' extend by 2 cells outside the physical domain and it is assumed that the mappings exist there. The determinants (J) are determined on the cells of boxes with size ghostBox+1. This is labeled a 'JReqGhostBox' herein. At domain boundaries, the boxes for 'J' extends by 1 cell outside the physical domain
-
Averages of fluxes. Most of the fluxes, <F>\ are stored as average quantities to be applied to a face and do not include area information. I.e., the actual flux across a 2-D face is
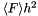 Hence when correcting from fine to coarse, you want to average the fine <F> and then muliply by the area of the coarse face (although in most equations, the area cancels out with another term). However, the
Hence when correcting from fine to coarse, you want to average the fine <F> and then muliply by the area of the coarse face (although in most equations, the area cancels out with another term). However, the 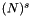 , which are a type of flux, are stored differently in that they have already been multiplied by the length term (equivalent to
, which are a type of flux, are stored differently in that they have already been multiplied by the length term (equivalent to 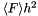 in the example above). Hence, these fluxes needed to be summed when correcting from coarse to fine.
in the example above). Hence, these fluxes needed to be summed when correcting from coarse to fine. - WARNING! If transverse components of <N> are computed analytically, they are only averaged down when finer levels have changed before entering a postTimeStep (along with normal components). Consequently, it is currently difficult to know if they have been computed or averaged from a finer level at any given point. But note that if transverse components of <N> are computed by averaging from normal components, then they should always be consistent. **FIXME – probably the best fix is to only average the normal components if transverse are computed analytically.
Member Enumeration Documentation
◆ AgeType
◆ TransverseNOpType
Constructor & Destructor Documentation
◆ LevelGridMetrics() [1/2]
| LevelGridMetrics::LevelGridMetrics | ( | const int | a_nComp, |
| const int | a_spaceOrder | ||
| ) |
Constructor.
◆ ~LevelGridMetrics()
|
virtual |
Destructor.
◆ LevelGridMetrics() [2/2]
|
private |
Member Function Documentation
◆ operator=()
|
private |
◆ clear()
| void LevelGridMetrics::clear | ( | ) |
Free memory.
◆ hasFiner()
| bool LevelGridMetrics::hasFiner | ( | ) | const |
Does a finer level exist?
◆ hasCoarser()
| bool LevelGridMetrics::hasCoarser | ( | ) | const |
Does a coarser level exist?
◆ define() [1/2]
| void LevelGridMetrics::define | ( | AMRLevel *const | a_AMRLevel, |
| MultiBlockCoordSysFactory *const | a_coordSysFact, | ||
| LevelGridMetrics *const | a_coarserLevelGridMetrics, | ||
| const RealVect & | a_dxVect, | ||
| const IntVect & | a_ghostVect, | ||
| const TransverseNOpType | a_transverseNOpType = TransverseNOpNone, |
||
| const bool | a_haveMultiBlockVectorData = true, |
||
| const int | a_numBlocks = 1 |
||
| ) |
Define the class. No metrics terms are yet available.
◆ define() [2/2]
| void LevelGridMetrics::define | ( | AMRLevel *const | a_AMRLevel, |
| MultiBlockCoordSys *const | a_coordSys, | ||
| LevelGridMetrics *const | a_coarserLevelGridMetrics, | ||
| const RealVect & | a_dxVect, | ||
| const IntVect & | a_ghostVect, | ||
| const TransverseNOpType | a_transverseNOpType = TransverseNOpNone, |
||
| const bool | a_haveMultiBlockVectorData = true, |
||
| const int | a_numBlocks = 1 |
||
| ) |
Define the class. No metrics terms are yet available.
◆ metricsDefined()
|
inline |
Are the metrics defined on this level?
After preRegrid, this also indicates if a level is used.
- Returns
- T - yes.
◆ didFinerChange()
|
inline |
Did the metrics change on the finer mesh?
- Returns
- T - yes.
◆ getCoordSys() [1/2]
|
inline |
◆ getCoordSys2()
|
inline |
◆ getCoordSys() [2/2]
|
inline |
- Parameters
-
[in] box Assigned to this box
References getCoordSys().
◆ getBlock()
|
inline |
Get the block index.
- Parameters
-
[in] a_box Assigned to this interior box
- Returns
- Block index
◆ blockDomain()
|
inline |
Get a problem domain representing a block.
- Parameters
-
[in] a_box Assigned to this interior box [in] a_numGhost The number of ghosts that the box representing the block should be grown by before cropping. Cropping only occurs at boundaries defined by the physical domain
- Returns
- If singleblock, the problem domain. If multiblock, non-periodic problem domain representing the block
- Note
- If single block, the problem domain must be cached when the coordSys is defined
References CH_assert, Box::define(), and grow().
◆ dxVect()
|
inline |
Get the computational mesh spacing.
- Returns
- Mesh spacing in each direction
◆ postTimeStep()
| void LevelGridMetrics::postTimeStep | ( | ) |
After a time step, average down 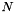 and
and 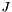 .
.
◆ initialGrid()
|
virtual |
Set up initial grid.
◆ postInitialGrid()
| void LevelGridMetrics::postInitialGrid | ( | const DisjointBoxLayout *const | a_newGrid | ) |
Set up the initial metric terms.
◆ preRegrid()
| void LevelGridMetrics::preRegrid | ( | const int | a_baseLevel, |
| const DisjointBoxLayout & | a_newGrid, | ||
| const LevelData< FArrayBox > *const | a_coarseUOldPtr, | ||
| LevelData< FArrayBox > & | a_UOld, | ||
| LevelData< FArrayBox > & | a_JUOld | ||
| ) |
Compute new metrics and correct the solution on the coarser meshes.
◆ regrid()
|
virtual |
Regrid operations – performs a coarse to fine interpolation.
◆ fillFineGhostCells()
|
virtual |
Fill invalid fine ghost cells (with preset CrFnU)
◆ computeValidU()
| void LevelGridMetrics::computeValidU | ( | LevelData< FArrayBox > & | a_U, |
| const LevelData< FArrayBox > & | a_JU | ||
| ) |
Computes <U> in valid cells.
◆ bufferSize4thO()
|
static |
Compute the minimum grid buffer size for a fourth-order interpolation.
◆ multiblockExchangeU()
| void LevelGridMetrics::multiblockExchangeU | ( | LevelData< FArrayBox > & | a_U, |
| const Interval & | a_vectorIntv | ||
| ) | const |
Exchange <U> across multiblock boundaries.
◆ timeIntermediate()
| void LevelGridMetrics::timeIntermediate | ( | const TimeInterpolatorRK4 & | a_timeInterpolator, |
| const Real & | a_timeInterpCoeff, | ||
| const int & | a_stage, | ||
| const Interval & | a_vectorIntv | ||
| ) |
Supports a call to TimeInterpolatorRK4::intermediate for multi-block grids.
◆ getBoxes()
|
inline |
Get the boxes.
◆ getDataIterator()
|
inline |
Get a level iterator.
References getBoxes().
◆ resizeWithGhosts()
Resize a box to include the ghost cells.
References grow().
◆ getJReqGhostVect()
|
inlinevirtual |
Determine the ghost vector required for 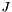 .
.
This is +1 over the ghost box to allow for derivatives needed to manipulate products
References IntVect::Unit.
◆ getNReqGhostVect()
|
inlinevirtual |
Determine the ghost vector required for 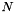 .
.
This is +2 over the ghost box to allow for tangential derivatives needed to compute the volume flux
References IntVect::Unit.
◆ resizeWithJReqGhosts()
Resize a box to the size required for 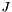 .
.
References grow().
◆ resizeWithNReqGhosts()
Resize a box to the size required for 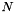 .
.
References grow().
◆ presetCr2ThisInterpolatorCrFnLevU()
Set the coarsened-fine <U> used by the interpolator (CrFn access)
Grids must have been defined for the interpolator. Returns a coarsening of 'this' level to be filled externally using a copyTo. 'this' is the fine level. I.e., 'this' is the fine level.
References CH_assert.
◆ presetCr2ThisInterpolatorCrFnLevJU()
Set the coarsened-fine <JU> used by the interpolator (CrFn access)
Grids must have been defined for the interpolator. Returns a coarsening of 'this' level to be filled externally using a copyTo. 'this' is the fine level. I.e., 'this' is the fine level.
References CH_assert.
◆ presetThis2FnInterpolatorCrFnLevU()
|
inline |
Set the coarsened-fine <U> used by the interpolator.
Grids must have been defined for the interpolator. Returns a coarsening of 'this' level. I.e., 'this' is the fine level.Grids must have been defined for the interpolator. Returns a coarsening of 'this' level. I.e., 'this' is the fine level.Grids must have been defined for the interpolator. Copies the coarse data from 'this' level to the coarsened-fine representation in the interpolator. 'this' is the coarse level.
- Parameters
-
[in] a_CrU <U> on the coarse level [in] a_vectorIntv An interval in components of U consisting of vector data
References CH_assert.
◆ invalidateCr2ThisInterpolatorCrFnLevData()
|
inline |
Invalidate the CrFn data, both <U> and <JU>\, used by the interpolator.
Grids must have been defined for the interpolator. Copies the coarse data from 'this' level to the coarsened-fine representation in the interpolator. 'this' is the coarse level.'this' is the fine level. If data goes out-of-date on the coarser level, then the interpolator, for interpolating to 'this' level, has out-of-date coarsened-fine data. There must be a coarser level
References CH_assert.
◆ invalidateThis2FnInterpolatorCrFnLevData()
|
inline |
Invalidate the CrFn data, both <U> and <JU>\, used by the interpolator.
'this' is the coarse level. If data goes out-of-date on 'this' level, then the interpolator, for interpolating to the next finer level, has out-of-date coarsened-fine data. You can invalidate even if there is no finer level.
◆ interpolatorCrFnNumGhost()
|
inline |
Number of ghosts used to build the coarsened-fine data in the interpolator.
- Parameters
-
[in] a_force T - avoid assertion checking. F - (default)
- Note
- The caller should ensure that a finer level exists if the assertion is disabled. Commonly, the return value is required inbetween initialGrid() and postInitialGrid() where the metrics have not yet been defined (so the assertion would fail) but the grid has been defined (so this value is known).
References CH_assert.
◆ isMultiblock()
|
inline |
Is this a multiblock grid.
- Returns
- T - Yes
◆ problemDomain()
|
inline |
◆ level()
|
inlineprotected |
◆ refRatio()
|
inlineprotected |
◆ verbosity()
|
staticprotected |
◆ defineMetrics()
|
protected |
Completely define the metrics for this level.
◆ undefineMetrics()
|
protected |
Label this and all finer levels as having undefined metrics.
◆ faceNormalN()
|
protected |
Compute 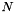 on the hyperfaces from
on the hyperfaces from 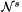 .
.
◆ getN()
Compute 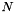 on the hyperfaces from
on the hyperfaces from 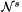 .
.
◆ faceTransverseN()
Add transverse components to 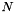 .
.
◆ getScriptN()
Integrate 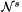 on each hyperedge.
on each hyperedge.
◆ averageScriptN()
|
protected |
Average 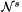 .
.
◆ averageN()
Average 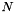 directly if
directly if 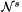 doesn't exist.
doesn't exist.
◆ getVolFlux()
|
protected |
Compute the volume flux.
◆ setAvgJfromNtX()
Take divergence of 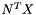 to set m_J.
to set m_J.
◆ averageVolFlux()
|
protected |
Average the volume flux 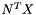 .
.
◆ volFluxCascade()
|
protected |
Compute 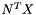 on all finer levels and average down.
on all finer levels and average down.
◆ averageSnapbackSolFlux()
|
protected |
Average the snapback solution flux, 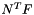 .
.
◆ defineGrids()
|
protectedvirtual |
Store the DisjointBoxLayout and define multiblock structures.
◆ defineGridsNP()
|
protected |
Create a non-periodic DisjointBoxLayout.
Member Data Documentation
◆ m_N
◆ m_J
Physical cell volume divided by computational cell volume
◆ m_scrNAverager
|
protected |
Averager for 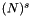 . Only used if m_useScriptN == true
. Only used if m_useScriptN == true
◆ m_NAverager
|
protected |
Averager for 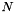 Only used if m_useScriptN == false
Only used if m_useScriptN == false
◆ m_NtXAverager
|
protected |
This averages the volume flux from a finer level. Averagers exist for old "AgeOld" and new "AgeNew" meshes during a regrid
◆ m_NtFDiffAverager
|
protected |
Averager for the snapback solution flux. This averager only operates on the intersections of three layouts.
◆ m_coordSys
|
protected |
The multi-block coordinate system.
◆ m_finerLevelGridMetrics
|
protected |
Grid metrics on the next finer level.
◆ m_coarserLevelGridMetrics
|
protected |
Grid metrics on the next coarser level
◆ m_parentAMRLevel
◆ m_ghostVect
|
protected |
Ghost cell vector.
◆ m_grids
|
protected |
Grid layout.
◆ m_gridsNP
|
protected |
Non-periodic grid layout. This is a shallow copy of m_grids, with a non- periodic problem domain and a new neighbor iterator if problemDomain() is periodic.
◆ m_dxVect
|
protected |
Mesh spacing in each direction.
◆ m_spaceOrder
|
protected |
Spatial-order of accuracy - must be 4.
◆ m_interpolator
|
protected |
Constrained least-squares interpolator for interpolating <JU> from coarse to fine meshes. 'This' mesh is the coarse mesh.
◆ m_cachedBlockDomain
|
protected |
Representing only the block (it is assumed periodic boundaries are not used for multiblock)
◆ m_cachedBlockIdx
|
protected |
Index of the cached block.
◆ m_cachedBlockNG
|
protected |
Number of ghosts that the cached block was grown by.
◆ m_mbgeo
|
protected |
Topology of the multiblock layout.
◆ m_mbex
|
protected |
To exchange information across multiblock boundaries
◆ m_Nmbreg
|
protected |
Flux-like register for resolving 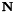 on faces at coarse- fine interfaces that overlap multiblock boundaries
on faces at coarse- fine interfaces that overlap multiblock boundaries
◆ m_NtXmbreg
|
protected |
Flux-like register for resolving 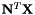 on faces at coarse-fine interfaces that overlap multiblock boundaries
on faces at coarse-fine interfaces that overlap multiblock boundaries
◆ m_transverseNOpType
|
protected |
Type of operatation for computing transverse terms in N
◆ m_metricsChanged
|
protected |
T - The metrics on this level have changed
◆ m_metricsDefined
|
protected |
T - The metrics have been defined for this level
◆ m_useScriptN
|
protected |
For some mappings, it is not possible to define scriptN. In those cases, N is calculated and averaged directly. The solution is conservative but freestream- preservation is lost across coarse- fine interfaces. T - Script N is used (default). F - Script N is not used. N is calculated directly and freestream preservation is lost
◆ m_isMultiblock
|
protected |
T - A multiblock coordinates system.
◆ m_haveMultiBlockVectorData
|
protected |
T - Space vector data will be exchanged across multiblock boundaries
◆ s_verbosity
|
staticprotected |
The documentation for this class was generated from the following file:
 1.8.13
1.8.13