Supporting classes and routines for FourthOrderMappedFineInterp. More...
#include <cstring>#include "NamespaceHeader.H"#include "NamespaceFooter.H"
Go to the source code of this file.
Classes | |
| class | CoordTransform |
| Coordinate transformations. More... | |
Macros | |
| #define | _FOURTHORDERMAPPEDFINEINTERPSUP_H_ |
Functions | |
| int | binomial (const int n, int k) |
| Calculate a binomial coefficient. More... | |
| int | powerIndex (int a_m, IntVect a_p) |
| Find the sequential index of a power. More... | |
Detailed Description
Supporting classes and routines for FourthOrderMappedFineInterp.
Macro Definition Documentation
◆ _FOURTHORDERMAPPEDFINEINTERPSUP_H_
| #define _FOURTHORDERMAPPEDFINEINTERPSUP_H_ |
Function Documentation
◆ binomial()
|
inline |
Calculate a binomial coefficient.
- Parameters
-
[in] n [in] k
- Returns
- Binomial coefficient
References CH_assert.
Referenced by powerIndex().
◆ powerIndex()
|
inline |
Find the sequential index of a power.
The powers are indexed as follows (i.e for 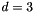 dimensions)
dimensions)
* int idx = 0 * for (px = 0; px <= m; ++px) * for (py = 0; px+py <= m; ++py) * for (pz = 0; px+py+pz <= m; ++py) * ++idx
where 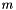 is the degree of the polynomial and we wish to find idx. To compute the sequential index of any given power, we can use the relations
is the degree of the polynomial and we wish to find idx. To compute the sequential index of any given power, we can use the relations
![\[ \mbox{number of powers} = {m + d \choose d} \]](form_27.png)
and
![\[ \sum_{j=k}^n {j\choose k} = { n+1 \choose k+1 } \]](form_28.png)
With these, the amount to add to the sequential index for a power at a spatial index is total number of powers remaining at this spatial index (remainder of 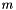 ) minus the number of powers not used at this spatial index. E.g, if
) minus the number of powers not used at this spatial index. E.g, if 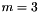 ,
, 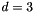 , and
, and 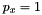 , there are 2 powers left for the remaining 2 dimensions,
, there are 2 powers left for the remaining 2 dimensions,
![\[ {2+2 \choose 2}\,. \]](form_31.png)
The increment to the sequential index is then
![\[ {2+3+1 \choose 2+1} - {2+2+1 \choose 2+1} \]](form_32.png)
In general, this can be written for direction index 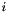 , in
, in 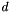 space dimensions, with
space dimensions, with 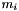 giving the remaining available powers at
giving the remaining available powers at 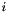 , and
, and  giving the power used at index
giving the power used at index 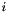 as
as
![\[ {d-i+m_i \choose d-i} - {d-i+m_i-p_i \choose d-i } \,. \]](form_37.png)
- Parameters
-
[in] a_m Degree of the polynomial [in] a_p Power for each direction
- Returns
- Sequential index
References binomial(), and SpaceDim.
 1.8.13
1.8.13